
A prímszámok azok a pozitív egészek, amelyeknek pontosan két osztójuk van: az 1 és önmaguk. Kis számoknál könnyű eldönteni, hogy egy szám prím-e, egyszerűen kipróbálhatjuk az összes lehetséges osztót, sőt elég csak a prímekkel való oszthatóságot vizsgálni gyök N-ig. Amikor viszont egy szám több ezer számjegyből áll, a helyzet gyökeresen megváltozik. Egy 2026 jegyű szám esetén például naiv ötlet a lehetséges osztók próbálgatása, mert ez annyira sok lépést igényelne, hogy erre az univerzum eddigi életkora sem volna elég. Emiatt a nagy prímek keresése és ellenőrzése teljesen más gondolkodást igényel.
Ha valaki egy 2026 jegyű prímet szeretne keresni, akkor elméletben megtehetné, hogy véletlenszerűen generál 2026 jegyű számokat, és ezeket teszteli. A prímszámtétel szerint N környékén 1/ln(N) valószínűséggel találunk prímet, ami ebben az esetben azt jelenti, hogy átlagosan néhány ezer jelölt közül csak egy lesz valóban prím. Itt azonban a tesztelés – az említett okok miatt – nem az osztók végigpróbálását jelenti, hanem egy többlépcsős folyamatot: először gyors szűréseket és valószínűségi prímteszteket futtatunk, amelyek gyorsan kiszórják az összetett számok döntő többségét. Ha a jelölt átmegy ezeken a teszteken, akkor mondhatjuk rá, hogy nagy valószínűséggel prím, de ez még nem teljes bizonyosság, szükség van még egy minden kétséget kizáró bizonyításra.
Ehhez úgynevezett prím-bizonyító algoritmusokra van szükség. Az elliptikus görbéken alapuló módszer (ECPP) ebbe a kategóriába tartozik: ha sikerrel jár, akkor nemcsak kijelenti, hogy a szám prím, hanem egy ellenőrizhető tanúsítványt is előállít. Ennek az ellenőrzéséből logikailag következik a prímség, így a végeredmény nem hit kérdése többé, hanem reprodukálható bizonyítás. A gyakorlatban az a tapasztalat, hogy ha egy szám már átment a gyors szűréseken és prímteszteken, akkor az ECPP nagyon sok esetben ténylegesen elő tudja állítani ezt a bizonyítványt, bár a futásideje változó.
Szemléletesen úgy lehet elképzelni a különbséget a próbálgatás és a bizonyítás között, mint egy bírósági eljárást. Az osztók egyenkénti keresése olyan lenne, mintha minden lehetséges gyanúsítottat külön-külön kihallgatnánk. A modern prím-bizonyítás ezzel szemben inkább egy döntő bizonyítékot keres, amelyből következik, hogy a szám nem lehet összetett. Ez a bizonyítvány gyakran úgy épül fel, hogy a nagy szám prímségét néhány gondosan választott köztes állításon keresztül visszavezeti kisebb számok prímségére. A bizonyítvány ellenőrzése gyors, függetlenül attól, hogy maga a szám milyen hatalmas.
Ha csak egyetlen nagy prímet szeretnénk találni, ezen a folyamaton önmagában nem lehet sokat gyorsítani. A nagy prímekre azonban sok területen szükség van – például a modern titkosítási eljárásokban –, ezért a gyakorlatban nem egyetlen számot, hanem sok jelöltet vizsgálunk egyszerre. Itt válik fontossá, hogy a keresés hatékonyságát növeli, ha olyan számcsaládokban dolgozunk, ahol a jelöltek tömegesen és olcsón szűrhetők. Ilyenek például az ismétlődő vagy majdnem ismétlődő számjegyekkel rendelkező számok. Ezek nem azért érdekesek, mert közöttük gyakoribbak lennének a prímek, hanem azért, mert sok kicsi prímmel való oszthatóságuk periodikus mintázatot mutat, így rengeteg jelöltet lehet egyszerre kizárni, mielőtt a drágább tesztekhez jutnánk. A szitálás után már csak kevés jelölt marad, és ezek közül néhány valóban prímnek bizonyulhat.
Ilyen módszerrel talált Ray Chandler 2012-ben egy 2026 jegyű prímszámot a (17⋅10n − 77)/3 alakú számok családjában (56w41). A szóban forgó 2026 jegyű számot n = 2025-re kapjuk. A szám tízes számrendszerben 5-tel kezdődik, utána nagyon sok 6-os következik (2023 db), és 41-re végződik. Az alábbi feladványban is ez a 2026 jegyű szám fog szerepelni.
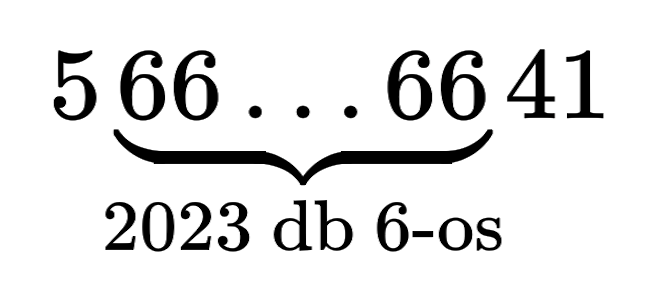
284. feladvány: 2026 jegyű prím
Mutassuk meg, hogy az 5…41 szám, ahol a … helyén 2023 darab 6-os áll, nem osztható se 13-mal, se 113-mal, se 1013-mal!
Keressünk olyan 10 hatványt, aminek az adott prímszámmal (13, 113 vagy 1013) vett osztási maradéka +1 vagy -1.
Mint ahogy az a bevezetőben megemlítésre került, a szóban forgó szám (17⋅102025 − 77 )/3 alakba is előáll. Ha pedig ezt az alakot nézzük, akkor elegendő a számláló oszthatóságát nézni mind a 13, mind a 113 mind pedig az 1013 tekintetében.
Mivel 7⋅13 = 1001, ezért 103-nak a 13-al vett osztási maradéka 12, amit úgy szoktak jelölni, hogy 103 ≡ 12 vagy 103 ≡ -1 (mod 13). Itt egyenlőség helyett a kongruencia ≡ jelét használjuk, ami a kongruencia jel két oldalán lévő számok azonos maradékát fejezi ki, a (mod 13) pedig azt jelöli, hogy 13-mal vett osztási maradékokról beszélünk. A fenti egyenlet mindkét oldalát négyzetre emelve azt kapjuk például, hogy 106 ≡ +1 (mod 13), vagyis 106-nak a 13-mal vett osztási maradéka 1, amit egyébként ellenőrizhetünk is: 76923⋅13 = 999999. Ha valami 1-et ad osztási maradékul, az azért hasznos nekünk, mert akárhányszor szorozzuk önmagával továbbra is 1-et fog adni, tehát 106 hatványaira is igaz, hogy 13-mal vett osztási maradékuk 1. Mármost 337⋅6 = 2022, tehát 102022 ≡ +1 (mod 13). Minket viszont 102025 maradéka jobban érdekel, ezért mindkét oldalt szorozzuk még 103-nal, és így kapjuk, hogy: 102025 ≡ -1 (mod 13). Innen pedig 17⋅102025 − 77 ≡ -17 – 77 = -94 ≡ -3 (mod 13). Vagyis a számláló 13-mal osztva 10 maradékot ad, vagyis nem osztható 13-mal, és így a vizsgált szám sem.
Hasonló stratégiát lehet követni a 113-mal való oszthatóság vizsgálatakor, de most bevetünk még valamit. A kis Fermat-tétel miatt tetszőleges p prímre és bármely a egész számra a(p-1) ≡ 1 (mod p). Ha most p = 113 és a = 10 esetén nézzük ezt, akkor kapjuk, hogy 10112 ≡ 1 (mod 113). Mármost 18⋅112 = 2016, ezért 102016 ≡ 1 (mod 113), tehát 102025 ≡ 109 ≡ 59 (mod 113). És így a számlálóra: 17⋅59 − 77 = 926 ≡ 22 (mod 113). Tehát a számláló nem osztható 113-mal, és így a vizsgált szám sem.
1013-mal való oszthatóságnál megint használhatjuk a kis Fermat-tételt, és most gyorsan célhoz jutunk. 101012 ≡ 1 (mod 1013), tehát 102024 ≡ 1 (mod 1013), amiből 102025 ≡ 10 (mod 1013), innen pedig a számlálóra az alábbi maradékot kapjuk: 17⋅10 − 77 = 170 − 77 = 93, tehát nem osztható 1013-mal.
Ha szereted a fejtörőket, tekintsd meg korábbi feladványainkat is! Ha megjegyzésed lenne, vagy feladványt javasolnál, írj az eszventura@qubit.hu e-mail címre! Ha pedig tetszik a rovat, ezt a Vendégkönyvben kifejezésre juttathatod.
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.



















